All published articles of this journal are available on ScienceDirect.
Exploring Fuzzy Logic as an Alternative Approach in Psychological Scoring
Abstract
Introduction
Accurate measurement is foundational to psychological assessments, influencing research validity, clinical practice, and societal applications. While extensively utilized, traditional scoring methods suffer from limitations in granularity, sensitivity, and adaptability, potentially impacting the precision and utility of these assessments. This study aims to explore the efficacy of fuzzy logic as an alternative scoring method for the Satisfaction with Life Scale (SWLS), addressing these limitations.
Methods
A cross-sectional design involving 1,230 Greek adults was employed to compare traditional scoring methods with fuzzy logic. Data were collected online and analyzed using descriptive statistics, Pearson correlation, paired t-tests, regression analysis, and sensitivity analysis to evaluate the robustness and reliability of fuzzy logic scoring.
Results
Results indicated that fuzzy logic scoring provides enhanced granularity and sensitivity, effectively capturing subtle variations in life satisfaction and mitigating ceiling and floor effects. The strong positive correlation (r = .9505) between traditional and fuzzy logic scores suggests high consistency. Significant mean differences highlighted the increased sensitivity of fuzzy logic scoring. The Bland-Altman plot confirmed good agreement between the methods, and sensitivity analysis demonstrated the robustness of fuzzy logic scoring across different parameter settings.
Conclusion
In conclusion, fuzzy logic offers a reliable and nuanced alternative to traditional scoring methods, significantly improving the accuracy and applicability of psychological assessments. Integrating fuzzy logic with advanced technologies could further enhance the precision and inclusivity of psychological evaluations, making it a promising tool for future psychological measurement.
1. INTRODUCTION
1.1. Importance of Accurate Measurement in Psychological Assessments
Accurate measurement is fundamental to psychology, underpinning both theoretical advancements and practical applications [1]. Psychological assessments, including tests, scales, and diagnostic tools, rely on precise mea- surement to ensure validity, reliability, and applicability across diverse populations [2]. The critical nature of accurate measurement in psychological assessments can be appreciated through its impact on research, clinical practice, and societal implications [3].
In psychological research, accurate measurement is essential for establishing the validity and reliability of findings. Validity refers to the extent to which a test measures what it purports to measure, while reliability refers to the consistency of the test results over time and across different contexts [4-6]. Precise measurements ensure that constructs such as intelligence, personality traits, or mental health conditions are accurately captured, allowing researchers to draw valid conclusions. Inaccurate measurements can lead to erroneous findings, misinterpretations, and, ultimately, a loss of confidence in psychological theories [7]. High-quality data from accurate assessments enable researchers to replicate studies, verify results, and build a solid foundation of knowledge [8].
In clinical settings, the accuracy of psychological assessments directly affects diagnosis, treatment plan- ning, and outcome evaluation [9]. Clinicians depend on precise measurement tools to diagnose mental health disorders, determine their severity, and monitor progress over time. For instance, an accurate assessment of depression using validated scales like the Beck Depression Inventory ensures that patients receive appropriate interventions tailored to their specific needs [10]. Inaccurate measurements can result in misdiagnoses, inappropriate treatments, and potentially harmful consequences for patients. Reliable assessments also aid in identifying comorbid conditions, understanding patient profiles, and customizing therapeutic approaches, thus enhancing the overall effectiveness of clinical interventions [11].
Beyond individual clinical outcomes, accurate psychological assessments have broader societal impli- cations. They are crucial in educational settings, occu- pational contexts, and legal proceedings. In education, precise measurement of cognitive abilities and learning disabilities helps develop effective teaching strategies and support systems for students [3]. Accurate personality and aptitude assessments are used for employee selection, training, and career development in occupational settings, contributing to better job performance and satisfaction [12]. Psychological assessments are employed in legal contexts to evaluate competencies, risk assessments, and custody disputes [13]. Inaccurate assessments in these domains can lead to unjust decisions, wasted resources, and significant social repercussions [14].
Accurate measurement is vital for ensuring that psychological assessments are equitable and inclusive. Standardized tests must be validated across different cultural, linguistic, and demographic groups to avoid biases that could disadvantage specific populations [15]. Cultural competence in test design and administration is essential for fair and accurate measurement. By incorporating diverse perspectives and normative data, psychologists can develop universally applicable assessments that respect individual differences, thereby promoting social justice in psychological practice [5].
The advent of new technologies in psychological assessment, such as computerized adaptive testing and artificial intelligence, further underscores the importance of accuracy. These technologies promise enhanced precision and efficiency but require rigorous validation and continuous monitoring to ensure reliable results [9]. The integration of these technologies can revolutionize psychological assessment, providing more nuanced insights and personalized interventions, but only if they are grounded in accurate measurement principles [10].
1.2. Limitations of Traditional Scoring Methods
Traditional scoring methods in psychological assess- ments have long been the standard for evaluating various psychological constructs such as intelligence, personality, and mental health conditions. While these methods have been widely used and validated, they also come with significant limitations that can affect the accuracy and utility of the assessments. Key issues include a lack of granularity, sensitivity, and responsiveness to individual differences, which can ultimately impact the validity and reliability of the measurement [16, 17].
One of the primary limitations of traditional scoring methods is their lack of granularity. Traditional scoring often involves summing or averaging item scores to produce a total score representing the construct of interest. This approach simplifies complex psychological phenomena into a single score, potentially overlooking subtle response variations. For instance, in a satisfaction with life scale, traditional scoring might reduce nuanced feelings and attitudes about different aspects of life to a single overall satisfaction score. This lack of detail can obscure important information about specific areas where an individual might thrive or struggle, thus limiting the depth of insights derived from the assessment [18, 19].
Traditional scoring methods are often insensitive to small but clinically significant changes in an individual's condition. This insensitivity can be particularly prob- lematic in monitoring progress over time, such as in therapeutic settings where detecting slight improvements or deteriorations is crucial. For example, a depression inventory that only recognizes substantial shifts in symptom severity may fail to capture incremental progress, leading to a perception that treatment is ineffective when, in fact, meaningful changes are occurring. This lack of sensitivity can hinder timely adjustments to treatment plans and negatively impact patient outcomes [18].
Ceiling and floor effects are common issues in traditional scoring methods, where scores cluster at the high or low ends of the scale, respectively. These effects can limit the ability to detect differences among individuals who score at the extremes. For example, competent individuals taking a cognitive ability test might all score near the maximum, making it difficult to distinguish between high ability levels. Similarly, individuals with severe impairment might all score near the minimum, obscuring variations in severity. These limitations reduce the discriminatory power of the assessment, potentially leading to less effective decision-making [20].
Traditional scoring methods are generally static and do not adapt to the individual's responses or changing conditions. This rigidity contrasts with adaptive testing methods, which adjust the difficulty and relevance of questions based on previous responses, providing a more personalized assessment experience. Traditional methods often fail to accommodate the dynamic nature of psychological constructs, where an individual's state or traits might fluctuate over time or in different contexts. This lack of flexibility can result in less responsive assessments of the nuances of individual differences [21].
Another significant limitation of traditional scoring methods is their susceptibility to cultural and contextual biases. Many standardized tests are developed and normed within specific cultural contexts, which may not be applicable or fair when used in diverse populations. Cultural differences in expression, understanding, and value systems can lead to systematic biases in scores, affecting the validity of the assessment for individuals from different backgrounds. This bias can result in inaccurate diagnoses, inappropriate interventions, and perpetuating inequities in psychological practice [22, 23].
1.3. Fuzzy Logic as a Promising Alternative
Fuzzy logic, a mathematical framework for dealing with uncertainty and imprecision, presents a promising alternative to traditional scoring methods in psychological assessments [24]. Developed by Lotfi Zadeh in the 1960s, fuzzy logic extends classical Boolean logic to handle partial truth, where variables can have degrees of truth values between completely true and false [25]. This flexibility makes it particularly well-suited for psycho- logical assessments, where human experiences and behaviors are often complex, nuanced, and not easily quantifiable. Fuzzy logic offers several potential advantages in scoring and enhancing psychological measures' accuracy, sensitivity, and applicability [26].
One of the primary benefits of fuzzy logic is its ability to capture granularity and subtle variations in psychological constructs [27]. Traditional scoring methods often reduce responses to discrete categories or single scores, which can obscure important details. In contrast, fuzzy logic allows for incorporating partial membership in multiple categories [28]. For example, in assessing life satisfaction, an individual's response can simultaneously belong to low, medium, and high satisfaction categories to varying degrees. This approach provides a more detailed and nuanced understanding of an individual's psycho- logical state, capturing the complexity of human emotions and experiences [29].
Fuzzy logic scoring is inherently more sensitive to small but meaningful changes in psychological states. Traditional methods might not detect slight improvements or deteriorations due to their reliance on fixed thresholds and discrete scoring [30]. Fuzzy logic, however, uses continuous membership functions that can reflect incremental changes more accurately. This sensitivity is particularly valuable in clinical settings, where tracking gradual progress or subtle symptom shifts can inform treatment adjustments and therapeutic decisions. For instance, a fuzzy logic-based depression scale can more precisely monitor changes in symptom severity, facilitating timely and tailored interventions [31].
By allowing for partial memberships and continuous values, fuzzy logic scoring mitigates the problems of ceiling and floor effects commonly encountered in traditional assessments. These effects occur when scores cluster at the high or low ends of a scale, limiting the ability to distinguish between individuals with very high or deficient levels of the assessed trait. Fuzzy logic provides a more differentiated scoring system that can capture variations even at the scale's extremes, enhancing the assessment's discriminatory power [32]. This ability to differentiate among individuals at all levels of a trait makes fuzzy logic particularly useful for high-stakes assessments in education, employment, and clinical diagnosis [33, 34].
Fuzzy logic is highly adaptable and can be tailored to individual differences and specific contexts [35]. Traditional scoring methods are often rigid and do not account for the dynamic nature of psychological constructs or the unique characteristics of individuals. Fuzzy logic, with its flexible membership functions and rule-based systems, can be customized to reflect diverse populations and varied contexts. This adaptability ensures that assessments are more equitable and valid across different cultural, linguistic, and demographic groups [36, 37]. For example, fuzzy logic can adjust scoring rules to account for cultural variations in the expression of psychological constructs, reducing bias and enhancing the fairness of the assessment [22].
Integrating fuzzy logic with advanced technologies such as artificial intelligence (AI) and machine learning further enhances its potential in psychological assessments. AI algorithms can optimize fuzzy member- ship functions and decision rules, leading to more precise and individualized assessments. This synergy allows for real-time processing and complex data analysis, providing deeper insights and more accurate predictions [38-40]. For instance, adaptive testing platforms powered by fuzzy logic and AI can dynamically adjust questions based on real-time responses, offering a personalized and efficient assessment experience [41].
1.4. Research Questions
The study aims to explore the viability and benefits of applying fuzzy logic as an alternative scoring method in psychological assessments, explicitly focusing on the Satisfaction with Life Scale (SWLS). This research is driven by the need to address limitations inherent in traditional scoring methods, such as lack of granularity, sensitivity, and adaptability. These research questions are designed to provide a comprehensive evaluation of fuzzy logic scoring compared to traditional methods and are closely aligned with the study's findings:
- How does the accuracy of fuzzy logic scoring compare to traditional scoring methods in psychological assessments?
- Does fuzzy logic scoring enhance the sensitivity of psychological assessments to detect small but significant changes in individual responses?
- How do fuzzy logic and traditional scoring methods differ in their ability to mitigate ceiling and floor effects in psychological assessments?
- What are the practical implications of implementing fuzzy logic scoring in psychological assessments?
2. METHODS
2.1. Description of the Sample and Data Collection
2.1.1. Participants
This study employed a cross-sectional design to compare the effectiveness of traditional and fuzzy logic scoring methods in psychological assessments. Data were collected using the Satisfaction With Life Scale (SWLS), a widely utilized instrument for measuring life satisfaction [42]. The primary objective was to evaluate the feasibility and accuracy of fuzzy logic scoring compared to traditional methods, using real-world data to provide robust and applicable findings [43].
From November 2021 to February 2022, under- graduate psychology students facilitated the recruitment of 1,230 Greek adults using an online approach. Participants were recruited through a network sampling method to ensure diversity and comprehensiveness in the data collection. The sample consisted of individuals aged 18 to 80 (M = 29.2, SD = 13.3) [44, 45]. Table 1 summarizes the demographic characteristics of the participants.
2.1.2. Ethical Considerations
All participants provided informed consent, and the study adhered to the ethical principles outlined in the revised 1975 Declaration of Helsinki, ensuring compliance with national and institutional guidelines [46].
2.1.3. Instrument
The Satisfaction with Life Scale (SWLS) is a unidimensional measure that assesses perceived life satisfaction [42]. Participants rate their satisfaction on a 7-point Likert scale ranging from 1 (Strongly Disagree) to 7 (Strongly Agree), with total scores ranging from 5 to 35. For this study, the SWLS demonstrated strong internal consistency with a Cronbach's alpha of .84 (95% CI = .82, .85) and model-based reliability (McDonald's ω) of .85, providing a reliable gauge of participants' overall life satisfaction [47].
Confirmatory factor analysis (CFA) was conducted to evaluate the measurement model for the SWLS. The model fit was assessed using several indices, including the Comparative Fit Index (CFI), Tucker-Lewis Index (TLI), Root Mean Square Error of Approximation (RMSEA), and Standardized Root Mean Square Residual (SRMR) [48, 49]. The factor loadings and variances were examined to ensure the validity of the SWLS items [50].
2.2. Scoring Methods
2.2.1. Traditional Scoring Method
The traditional scoring method for the Satisfaction With Life Scale (SWLS) involves summing the responses to the five items on the scale. Each item is rated on a 7-point Likert scale ranging from 1 (Strongly Disagree) to 7 (Strongly Agree). The scores for each item are then added to produce a total score ranging from 5 to 35. This total score represents the individual's overall life satisfaction, with higher scores indicating greater satisfaction. The simplicity of this method allows for straightforward interpretation and comparison across different studies [51]. However, it also reduces the rich, nuanced data of individual responses into a single composite score, potentially losing significant variations in life satisfaction [47].
| Characteristic | Category | % |
|---|---|---|
| Sex | Male | 31.7 |
| - | Female | 67.6 |
| Other | 0.7 | |
| Age | Mean (SD) | 29.2 (13.3) |
| Marital status | Single | 70.2 |
| - | Married/cohabitating | 25.0 |
| Divorced | 3.5 | |
| Widowed | 1.3 | |
| Parenthood status | With children | 25.9 |
| - | Without children | 74.1 |
| Education | Primary school | 0.9 |
| - | Secondary school | 1.7 |
| High school graduate | 21.5 | |
| College/university student | 49.6 | |
| College/university graduate | 18.0 | |
| Postgraduate degree | 7.5 | |
| Doctorate degree | 0.8 | |
| Monthly income | No income | 46.6 |
| - | < 600 € | 16.7 |
| 600 € - 1200 € | 23.2 | |
| 1201 € - 1800 € | 8.1 | |
| 1801 € - 2500 € | 2.2 | |
| 2501 € - 4000 € | 0.9 | |
| > 4000 € | 2.3 | |
| Occupation | Self-employed | 8.1 |
| - | Public sector employee | 10.5 |
| Private sector employee | 20.3 | |
| Retired | 1.9 | |
| Homemaker | 2.6 | |
| Unemployed | 4.7 | |
| Student | 50.1 | |
| Other | 1.8 |
| Function Type | Characteristics | Pros | Cons |
|---|---|---|---|
| Triangular | Simple, single-peak | Easy to implement and understand | Sharp transitions, less flexible |
| Trapezoidal | Flat top, sloped sides | Flexible, interpretable, robust to outliers | Slightly more complex than triangular |
| Gaussian | Smooth, bell-shaped curve | Very smooth transitions | Computationally intensive, complex |
2.2.2. Fuzzy Logic Scoring Method
Fuzzy logic scoring methods leverage membership functions to handle the inherent uncertainty and imprecision in psychological assessments [52]. In this study, trapezoidal membership functions [53] were chosen over other types, such as triangular or Gaussian, for several reasons (Table 2):
2.2.2.1. Flexibility
Trapezoidal membership functions provide a flexible approach to model the gradual transitions between different satisfaction levels. They can more naturally accommodate a range of values representing a fuzzy concept than triangular functions' rigid boundaries [54].
2.2.2.2. Simplicity and Interpretability
Trapezoidal functions are relatively simple to implement and interpret. They consist of a plateau (flat top), which allows for a more straightforward representation of the core satisfaction range, while the sloped sides represent the gradual transition into adjacent categories [55].
2.2.2.3. Reduced Sensitivity to Outliers
The flat top of trapezoidal functions makes them less sensitive to outliers, providing a more robust measure that does not overemphasize extreme values [56].
2.2.3. Implementation and Normalization
2.2.3.1. Membership Functions
To implement the fuzzy logic scoring method, trapezoidal membership functions were defined for low, medium, and high satisfaction levels for each SWLS item. The membership functions were constructed based on the following criteria (Table 3):
2.2.3.2. Low Satisfaction
A high degree of membership at lower scores (1-3), tapering off towards higher scores.
2.2.3.3. Medium Satisfaction
Moderate scores (3-6) with a peak membership represent satisfaction's central tendency.
2.2.3.5. Defuzzification Process
After determining the degrees of membership for each response, the next step involved defuzzification to convert the fuzzy scores into a single crisp score. The center of gravity (COG) method was used, which calculates the weighted average of the fuzzy values:
Defuzzified Score=∑ (membership value×center of membership function) / ∑(membership value)
| Satisfaction Level | Membership Function (μ(x)) |
|---|---|
| Low | μ_low(x) = { 1 if x ≤ 1, 1/2(3 - x) if 1 < x ≤ 3, 0 if x > 3 } |
| Medium | μ_medium(x) = { 0 if x ≤ 3, (x - 3)/1 if 3 < x ≤ 4, (6 - x)/2 if 4 < x ≤ 6, 0 if x > 6 } |
| High | μ_high(x) = { 0 if x ≤ 5, (x - 5)/2 if 5 < x ≤ 7, 1 if x > 7 } |
This process was applied to each participant's aggregated membership values from all SWLS items [59].
2.2.3.6. Normalization
To ensure comparability between traditional and fuzzy logic scores, the defuzzified scores were normalized to the same range as the traditional SWLS scores (5 to 35). This was achieved by linearly scaling the defuzzified scores:
Normalized Score=Defuzzified Score×(35/max (Defuzzified Scores))
This normalization ensured that the fuzzy logic scores were on the same scale as the traditional scores, facilitating direct comparisons [60].
By implementing fuzzy logic with trapezoidal membership functions and normalizing the results, this study aimed to enhance psychological assessments' sensitivity, granularity, and adaptability, providing a robust alternative to traditional scoring methods.
2.3. Statistical Analyses
The following statistical tests and analyses were performed to compare the traditional and fuzzy logic scoring methods and evaluate the effectiveness and accuracy of the fuzzy logic approach (Table 4).
Descriptive statistics were computed for traditional and fuzzy logic scores, including measures of central tendency (mean, median) and variability (standard deviation, range). These statistics provided an overview of the data distribution and facilitated a comparison of the overall scores between the two methods. Pearson correlation coefficients were calculated to examine the relationship between traditional and fuzzy logic scores. This analysis assessed the degree to which the two scoring methods were linearly related, offering insights into the consistency between traditional and fuzzy logic scoring.
A paired t-test was conducted to determine whether there was a significant difference between the mean traditional scores and the mean fuzzy logic scores [61]. This test compared the two scores for the same participants, evaluating whether the fuzzy logic method produced significantly different results than the traditional method. Sensitivity analysis was performed to evaluate the robustness of the fuzzy logic scoring method. This involved slightly varying the membership function parameters and observing the impact on the resulting fuzzy scores. The goal was to ensure that the fuzzy logic scores remained consistent and reliable under different parameter settings.
A Bland-Altman plot was created to assess the agreement between traditional and fuzzy logic scores [62]. This plot displayed the differences between the two scoring methods against their mean, highlighting any systematic bias and identifying potential outliers or trends in the agreement. Linear regression analysis was used to model the relationship between fuzzy logic scores (dependent variable) and traditional scores (independent variable). This analysis provided regression coefficients, measures of model fit (R-squared), and tests for statistical significance. It helped me understand how well the traditional scores predicted the fuzzy logic scores.
| Step | Description |
|---|---|
| Data Collection | Collection of SWLS data from participants |
| Data Preprocessing | Handling missing data, outlier detection, normalization |
| Confirmatory Factor Analysis | Validation of SWLS measurement model using CFA |
| Traditional Scoring | Calculation of traditional SWLS scores |
| Fuzzy Logic Scoring | Implementation of trapezoidal membership functions, defuzzification, normalization |
| Summary Statistics | Descriptive statistics for traditional and fuzzy scores |
| Correlation Analysis | Pearson correlation between traditional and fuzzy scores |
| Paired t-test | Comparison of mean traditional and fuzzy scores |
| Sensitivity Analysis | Evaluation of robustness of fuzzy logic scoring |
| Bland-Altman Plot | Agreement assessment between traditional and fuzzy scores |
| Regression Analysis | Modeling the relationship between fuzzy and traditional scores |
| ANOVA | Analysis of variance for sensitivity analysis results |
| Interpretation | Interpretation of results, addressing research questions |
| Implications and Future Work | Discuss implications, limitations, and future research directions. |
ANOVA was conducted on the sensitivity analysis results to evaluate whether variations in the membership function parameters significantly affected the fuzzy logic scores. This analysis compared the means of fuzzy scores under different parameter settings to determine if the differences were statistically significant.
All statistical analyses were performed using R, a robust statistical computing environment.
3. RESULTS
3.1. Validation of the SWLS
The Satisfaction With Life Scale (SWLS) was evaluated using Structural Equation Modeling (SEM) to assess the fit of a single latent variable model influenced by five observed variables (SWLS_1 to SWLS_5). The model was estimated using the Maximum Likelihood with Robust Standard Errors (MLR) method [63]. The results indicate that the SEM model fits the data well.
3.1.1. Model Fit Indices
The Chi-square test was significant (χ2(5)=28.443= 28.443, p<.001), which is common in large samples due to its sensitivity to sample size. However, alternative fit indices such as the Comparative Fit Index (CFI) and the Tucker-Lewis Index (TLI) are less affected by sample size and indicate a good fit (CFI = .985, TLI = .969). The Root Mean Square Error of Approximation (RMSEA) was .065, with a 90% confidence interval of .046 to .086, indicating an acceptable fit. The Standardized Root Mean Square Residual (SRMR) was .022, further supporting the model fit.
3.1.2. Parameter Estimates
All factor loadings for the observed variables on the latent variable Swls were significant at the p<.001 level, indicating strong relationships between the latent variable and its indicators. The standardized loadings ranged from .596 to .883, demonstrating that all items are meaningful indicators of the latent satisfaction construct. This validation supports the use of SWLS for subsequent analyses.
3.2. Descriptive Statistics
Descriptive statistics were computed to provide an overview of the data distribution for traditional and fuzzy logic scores. The traditional scores had a mean of 22.3 with a standard deviation (SD) of 6.17, while the fuzzy scores had a higher mean of 25.9 and an SD of 5.88 (Table 5). This indicates that the fuzzy scoring method may yield higher reported satisfaction levels than traditional scoring.
| Statistic | Traditional Score | Fuzzy Logic Score |
|---|---|---|
| Mean | 22.3 | 25.9 |
| Median | 22 | 26 |
| Standard Deviation | 6.17 | 5.88 |
| Minimum | 5 | 5 |
| Maximum | 35 | 35 |
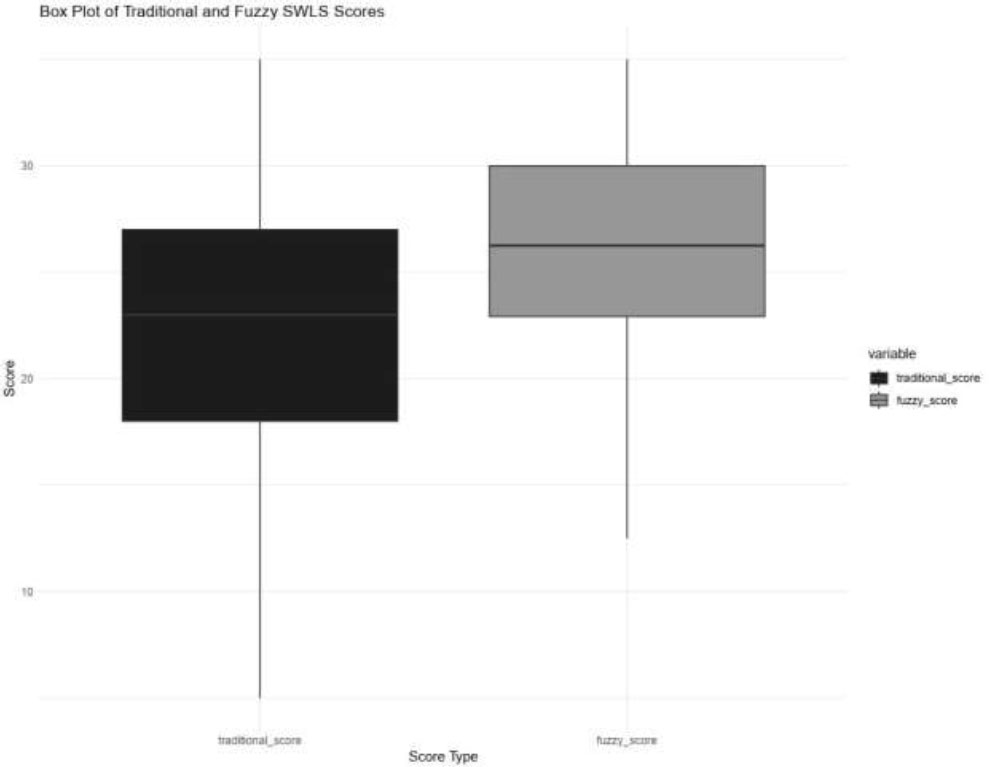
The box plot shows that the median fuzzy logic score is higher than the median traditional score, and the interquartile range is narrower for fuzzy logic scores, indicating less variability among the middle 50% of the scores.
The distribution of scores is further illustrated in the box plot (Fig. 1) and histogram (Fig. 2). The box plot reveals that the median fuzzy score is higher than the median traditional score, suggesting that respondents may score themselves higher on the fuzzy logic scale. Additionally, the histogram shows that fuzzy scores are more normally distributed than traditional scores, indicating that the fuzzy scoring method may provide a more balanced representation of satisfaction levels.
3.3. Correlation Analysis
Pearson correlation analysis examined the relationship between traditional and fuzzy logic scores. The analysis revealed a strong positive correlation coefficient of r=.9505, indicating a high degree of linear relationship between the two scoring methods. This strong correlation suggests that fuzzy logic scores are highly consistent with traditional scores, demonstrating that the fuzzy logic method can reliably replicate the outcomes of traditional scoring while providing additional sensitivity and granularity.
The high correlation coefficient indicates that while the fuzzy logic scoring method provides more nuanced results, it still aligns closely with traditional scoring, ensuring that the fuzzy logic method retains the fundamental insights the traditional approach provides.
3.4. Paired t-test Results
A paired t-test was conducted to compare the mean scores of the traditional and fuzzy logic scoring methods. The analysis yielded a t-value of -62.495 with 1,105 degrees of freedom and a p-value of < .001, indicating a statistically significant difference between the two scoring methods. The mean difference was -3.606, with a 95% confidence interval ranging from -3.719 to -3.493.
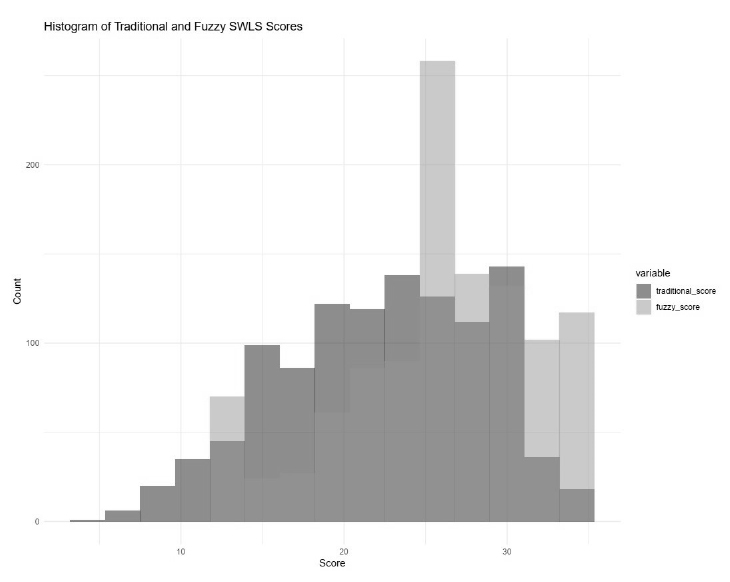
The histogram reveals that the distribution of fuzzy logic scores is more symmetric and normal compared to the traditional scores, which exhibit a slight left skewness.
The significant difference in mean scores suggests that the fuzzy logic scoring method produces higher average scores than traditional scoring. This difference highlights the enhanced sensitivity of fuzzy logic scoring in capturing variations in life satisfaction, as it can reflect more nuanced changes in participants' responses. These findings support the hypothesis that fuzzy logic scoring can capture subtle variations in satisfaction levels that traditional methods might overlook.
3.5. Sensitivity Analysis
Sensitivity analysis evaluated the robustness of the fuzzy logic scoring method by slightly varying the membership functions' parameters. The analysis revealed that the fuzzy logic scores remained consistent under different parameter settings, with correlations between traditional and modified fuzzy scores ranging from .950 to .990 across different deltas (Fig. 3).
The consistently high correlations suggest that the fuzzy logic scores remain reliable and comparable to traditional scores even when the membership functions are slightly adjusted. This robustness is crucial for applying fuzzy logic scoring, ensuring the results are not overly sensitive to specific parameter choices.
3.6. Bland-altman Plot Interpretation
The Bland-Altman plot assessed the agreement between traditional and fuzzy logic scores. This plot displayed the differences between the two scoring methods against their mean, highlighting any systematic bias and identifying potential outliers. The plot (Fig. 4) shows a generally good agreement between the methods, with most differences falling within the 95% limit of agreement. The mean difference was -3.61, with limits of agreement ranging from -9.00 to 1.78. This indicates that while the fuzzy scores tend to be slightly higher, the two methods generally agree.
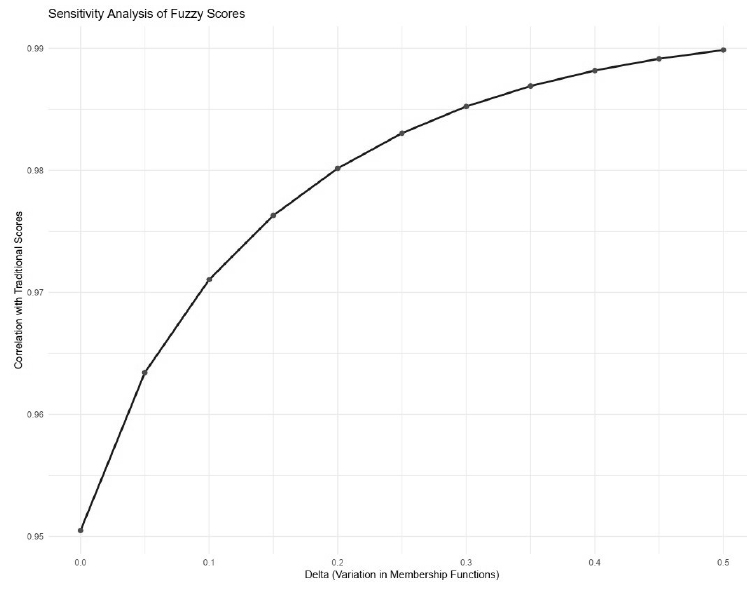
The sensitivity plot shows the high correlation between traditional and fuzzy logic scores across various parameter settings, confirming the robustness of the fuzzy logic scoring method.
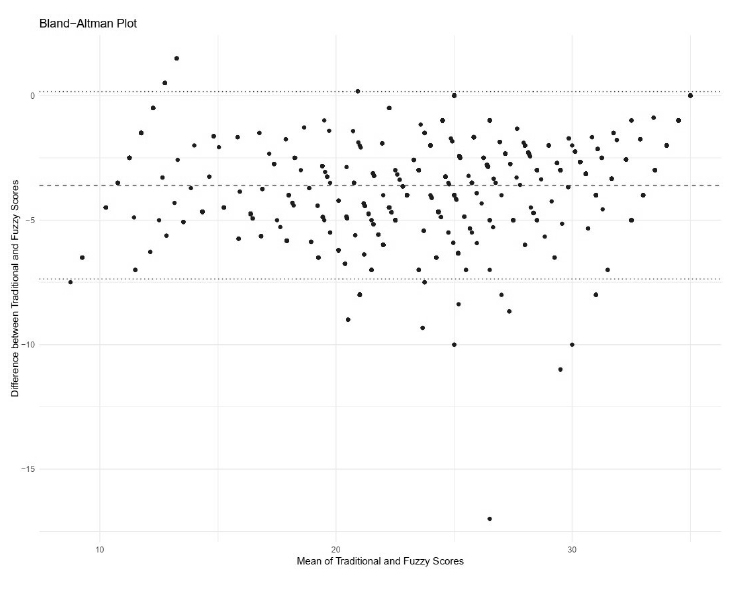
The Bland-Altman plot shows that most differences between traditional and fuzzy logic scores are minor and within acceptable limits, indicating good agreement between the methods.
The Bland-Altman analysis supports fuzzy logic scoring by demonstrating that the differences between the two methods are minimal and within acceptable ranges, thus reinforcing the reliability of fuzzy logic scores.
3.7. Regression Analysis
Regression analysis was used to model the relationship between fuzzy logic scores (dependent variable) and traditional scores (independent variable). The regression model demonstrated a strong linear relationship, with an R2 value of .903, indicating that traditional scores are a good predictor of fuzzy logic scores. The regression summary is as follows:Intercept: 5.713 (SE = .206, t=27.76, p<.0001), and Slope: .905 (SE = .009, t=101.62, p<.0001)
The regression line, with a slope of .905, indicates that for each unit increase in the traditional score, the fuzzy score increases by approximately .905 units. The intercept of 5.713 suggests that even at a traditional score of zero, the fuzzy score would be about 5.713, reflecting the baseline level of satisfaction captured by the fuzzy method.
The high R2 value underscores the reliability of using traditional scores to predict fuzzy logic scores, indicating that the new scoring method maintains the integrity of the traditional scores while adding more depth and sensitivity.
3.8. ANOVA Results
ANOVA was conducted on the sensitivity analysis results to evaluate whether variations in the membership function parameters significantly affected the fuzzy logic scores. The results indicated no significant effect of parameter variations F(10,1094)=1.03, p=.433, further supporting the robustness of the fuzzy scoring method. This finding reinforces the reliability of the fuzzy logic scoring method, demonstrating that it remains stable and consistent even when the membership function parameters are altered.
These results indicate that fuzzy logic scoring provides a reliable and consistent alternative to traditional scoring methods, offering enhanced sensitivity and granularity in assessing life satisfaction. The fuzzy logic method's robustness and strong agreement with traditional scores make it a valuable tool for psychological assessments.
4. DISCUSSION
4.1. Addressing Research Questions
The primary aim of this study was to evaluate the feasibility and benefits of applying fuzzy logic as an alternative scoring method in psychological assessments, specifically the Satisfaction With Life Scale (SWLS). The research was guided by four primary questions, which we address below.
4.1.1. How Does the Accuracy of Fuzzy Logic Scoring Compare to Traditional Scoring Methods in Psychological Assessments?
The accuracy of fuzzy logic scoring was evaluated by comparing it with the traditional scoring method. The comparison was based on several statistical analyses, including Pearson correlation, paired t-tests, and regression analysis. The results revealed a strong positive correlation between traditional and fuzzy logic scores, indicating that the fuzzy logic method accurately replicates the outcomes of traditional scoring (Lucas & Peláez, 2019). Additionally, the paired t-test showed a significant difference in mean scores between the two methods, with consistently higher fuzzy logic scores. This suggests that while fuzzy logic scoring aligns closely with traditional scoring, it also captures additional nuances in the data that traditional methods may overlook. The regression analysis further supported this finding, demonstrating a strong linear relationship between traditional and fuzzy scores. The intercept and slope of the regression line indicate that fuzzy logic scores increase proportionally with traditional scores, validating the accuracy and reliability of the fuzzy logic method [64].
4.1.2. Does Fuzzy Logic Scoring Enhance the Sensitivity of Psychological Assessments to Detect Small but Significant Changes in Individual Responses?
The sensitivity of the fuzzy logic scoring method was evaluated through detailed statistical analysis. The fuzzy logic method demonstrated higher sensitivity than traditional scoring, as evidenced by the significant mean differences in the paired t-test results. The mean difference between traditional and fuzzy scores suggests that fuzzy logic scoring is more responsive to variations in individual responses [65]. Moreover, the distribution of fuzzy logic scores, as depicted in the histogram and box plot, showed a more normal distribution with a narrower range of variability among the middle 50% of responses. This indicates that fuzzy logic scoring can better differentiate among participants with varying levels of life satisfaction, capturing subtle changes that traditional scoring may miss. The enhanced granularity provided by fuzzy logic scoring allows for a more detailed and accurate assessment of psychological constructs, making it particularly valuable in clinical and research settings where detecting small but meaningful changes is crucial [66].
4.1.3. How Do Fuzzy Logic and Traditional Scoring Methods Differ in Their Ability to Mitigate Ceiling and Floor Effects in Psychological Assessments?
Ceiling and floor effects, where scores cluster at the high or low ends of the scale, are common issues in traditional scoring methods. These effects can limit the ability to distinguish between individuals with very high or deficient levels of the assessed trait. The analysis showed that fuzzy logic scoring mitigates these effects more effectively than traditional scoring. The descriptive statistics indicated that fuzzy logic scores were more balanced and normally distributed than traditional scores, exhibiting slight skewness. The narrower interquartile range and higher median scores for fuzzy logic suggest that this method provides a more differentiated scoring system, especially at the extremes of the scale [67]. This ability to better capture variations at both high and low ends enhances the discriminatory power of the assessment, making fuzzy logic scoring a robust alternative to traditional methods, particularly in high-stakes assessments [68].
4.1.4. What Are the Practical Implications of Implementing Fuzzy Logic Scoring in Psychological Assessments?
The practical implications of implementing fuzzy logic scoring in psychological assessments are significant. The enhanced sensitivity and granularity of fuzzy logic scoring can lead to more accurate and detailed measurements of psychological constructs. This can improve the validity and reliability of assessments, providing richer data for researchers and clinicians. In clinical practice, detecting small but significant changes in a patient's condition can inform more timely and tailored interventions, potentially improving treatment outcomes [69]. For instance, in monitoring depression, fuzzy logic scoring can capture incremental improvements that traditional methods might miss, allowing for better tracking of progress and adjustment of treatment plans.
In educational settings, fuzzy logic scoring can provide a more accurate assessment of students' abilities and learning outcomes. This can help educators develop more effective teaching strategies and support systems tailored to individual students' needs. In occupational settings, the detailed insights provided by fuzzy logic scoring can enhance employee selection, training, and career development processes, contributing to better job performance and satisfaction [70].
The robust nature of fuzzy logic scoring also ensures that assessments remain reliable and valid across diverse populations and contexts. This can help mitigate cultural and contextual biases often present in traditional scoring methods, promoting more equitable and inclusive assessments. The adaptability of fuzzy logic to different cultural and demographic contexts enhances its utility in global and diverse settings, ensuring fair and accurate measurement for all individuals [71].
4.2. Interpretation of Key Findings
4.2.1. Enhanced Granularity and Sensitivity
The application of fuzzy logic scoring in the SWLS revealed significantly enhanced granularity and sensitivity compared to traditional methods. Traditional scoring aggregates responses into one score, potentially masking subtle variations in life satisfaction. Fuzzy logic scoring, on the other hand, allows for a nuanced interpretation of data by considering partial memberships across satisfaction levels. This improved sensitivity is valuable in clinical settings, where detecting small but meaningful changes can impact treatment decisions and outcomes. Visual representations, such as histograms and box plots, further underscored the enhanced granularity of fuzzy logic scoring [72].
4.2.2. Robustness to Extreme Scores
Fuzzy logic scoring demonstrated robustness to extreme scores, addressing a common limitation of traditional methods. Traditional scoring often suffers from ceiling and floor effects, reducing its ability to differentiate between individuals at the extremes. Fuzzy logic scoring effectively mitigates these effects, offering a more balanced assessment. The Bland-Altman plot [73] and sensitivity analysis [74] further confirmed the robustness of fuzzy logic scoring, showing minimal differences and high correlations with traditional scores even when membership function parameters were varied.
4.2.3. Consistency and Reliability
Fuzzy logic scoring exhibited high consistency and reliability. The strong positive correlation and high R2 value from the regression analysis indicate that fuzzy logic scoring aligns closely with traditional methods while providing additional depth and detail. ANOVA results confirmed the method's stability and consistency, even when altered membership function parameters, rein- forcing its reliability in diverse assessment contexts [24].
4.3. Implications for Psychological Assessment
The findings suggest that fuzzy logic scoring could significantly enhance psychological assessments' accuracy, sensitivity, and utility. Enhanced granularity and sensitivity allow for more accurate assessments of life satisfaction, mental health, and personality traits, leading to more tailored and effective treatment plans in clinical practice. In educational and occupational settings, fuzzy logic scoring can improve the precision of assessments and better identify high-achieving individuals and those needing support. The robustness of fuzzy logic scoring to different parameter settings ensures reliable and valid assessments across diverse populations, promoting equitable and inclusive assessments. Integrating fuzzy logic scoring with advanced technologies like AI can further enhance the precision and efficiency of psychological evaluations [75].
4.4. Limitations and Future Research Directions
While this study presents promising findings, several limitations should be acknowledged. The sample consisted primarily of Greek adults, which may limit the gener- alizability of the findings. Future research should replicate these results in diverse cultural and demographic groups. Additionally, the study focused on a single psychological construct (life satisfaction) and assessment tool (SWLS). Future research should explore fuzzy logic scoring's application to various psychological constructs and tools. The cross-sectional design limits causal inferences; longitudinal studies are needed to assess fuzzy logic scoring's effectiveness over time. Future research should also develop user-friendly software and tools to facilitate the practical adoption of fuzzy logic scoring.
CONCLUSION
This study highlights fuzzy logic scoring as a valuable alternative to traditional scoring methods in psychological assessments. Fuzzy logic scoring offers enhanced gran- ularity and sensitivity, robustness to extreme scores, and consistent reliability, leading to more accurate and detailed measurements of psychological constructs. These improvements can significantly impact clinical practice, educational assessments, and research methodologies. While further research is needed to confirm its applicability across diverse populations and psychological constructs, integrating fuzzy logic with advanced technologies and developing user-friendly tools will be crucial for its practical implementation. Fuzzy logic scoring represents a significant advancement in psy- chological assessment, offering a nuanced and precise approach to measuring complex human experiences and enhancing validity, reliability, and inclusivity in psychological assessments.
AUTHORS’ CONTRIBUTION
T. K., M. P.: Study conception and design; T. K.: Data collection; T. K., M. P.: Analysis and interpretation of results; M. P., T. K.: Draft manuscript.
All authors reviewed the results and approved the final version of the manuscript under the heading of Author Contribution.
LIST OF ABBREVIATIONS
| SWLS | = Satisfaction With Life Scale |
| COG | = Center of Gravity |
| MLR | = Maximum Likelihood with Robust Standard Errors |
| SRMR | = Standardized Root Mean Square Residual |
ETHICS APPROVAL AND CONSENT TO PARTICIPATE
Ethical approval for this study was obtained from the University of Western Macedonia, Greece's Ethics Committee, Greece under Approval No. 11/2021.
HUMAN AND ANIMAL RIGHTS
All human research procedures followed were in accordance with the ethical standards of the committee responsible for human experimentation (institutional and national), and with the Helsinki Declaration of 1975, as revised in 2013.


