The motivation behind writing this paper was a question which was frequently asked by the graduate students in an applied measurement course with a strong focus on validity and validation. The final project for the course was validating an instrument using any commonly accepted methodology in the literature. Those who chose to provide criterion related evidence had no problem in understanding why a high coefficient of correlation between their scale and an already existing test supports the validity of their tests. However, those who chose to use exploratory factor analysis or fit a confirmatory factor analysis model or the Rasch model had difficulty to appreciate why a good fit of their data to the model is considered validity evidence. An informal survey among colleagues who routinely used latent trait models for validating their instruments also showed that very few appreciate the logic of latent trait theory as evidence for test validity. The reason why the fit of data to a latent trait model counts as validity evidence for a test has been discussed in this paper. In this endeavor we draw on latent trait theory and latent variable analysis as delineated by Borsboom and his colleagues in a number of publications between 2003 to 2013.

The definition of validity has undergone many changes over the past few decades. Kelley [1] defined validity as the extent to which a test measures what it purports to measure. Guilford ([2], p. 429) argued that “a test is valid for anything with which it correlates”. Cronbach and Meehl [3] wrote the classic article Construct Validity in Psychological Tests where they divided validity into four types: predictive, concurrent, content and construct, the last one being the most important one.

Construct validity refers to the question of what constructs produce the reliable variance in test scores [3]. Cronbach and Meehl [3] state that when there is no criterion to correlate the test against and no adequate and accepted content to compare the content of the test with, construct validation should be carried out. In construct validation the test content and the power of scores to predict a criterion are not important. What is focal is the trait underlying the test.

Another important concept that Cronbach and Meehl [3] introduced is the nomological network. Nomological network refers to a system or a set of hypotheses that they assume to hold and relate the elements of the system. These elements within the system are ‘behaviour samples’ that should not necessarily be criteria according to Cronbach and Meehl [3]. The system actually exists in the mind of the researcher and is formed on the basis of experience, common sense, and expectation.

We start with a vague concept which we associate with certain observations. We then discover empirically that these observations covary with some other observation which possesses greater reliability or is more intimately correlated with relevant experimental changes than is the original measure, or both ([3], p. 286).

If empirical evidence, namely, coefficients of correlation support the theory, that is, if the nomological network holds then we can claim that both the test and the construct are valid, in other words, we have solicited support for both. However, if we cannot gain support for the theory, either the construct theory or the test, or both are invalidated and this requires modification of either the theory or the test, or both [4].

Messick [4] unified this componential conception of validity by asserting that validity is only one but at the same time expanded it by adding several other concepts under this unified multifaceted framework. Messick [4] defined validity as the appropriateness of inferences and interpretations based on test scores. According to this view of validity it is not the test that is validated but the inferences and decisions based on the test scores. Test interpretation and use, its potential social consequences, and their value implications are amongst the several components under this faceted concept.

Kane [5, 6] defines validity in the same way as Messick [4] did and proposes the argument-based approach to validity. In this approach, the researcher should gather adequate evidence to justify that the test is valid for a certain purpose. In this approach researchers first advance the interpretive/use argument, in which they delineate what interpretations and uses they are going to make on the basis of the test results, and then put forward the validity argument, where they accumulate evidence to support that the intended test uses envisaged in the first step are valid.

The validity concept advanced by Messick [4] and finely systematized by Kane [5, 6] in the argument-based approach has been criticized by Borsboom et al. [7, 8]. They adopt a realist stance on psychological constructs and invoke causation rather than correlation as a necessary condition to establish validity. They argue that validity is related to the instrument itself and researchers validate tests, not the inferences made on the basis of test scores. They state that validity is not multifaceted and complex and issues of test social consequences and inferences, though being important, are not related to validity. Validity is a simple concept as was defined by Kelley [1], i.e., the degree to which a test measures what it purports to measure.

Borsboom et al. [7] further argue that a test is valid if (a) the construct exists and (b) there is a causal relationship between the levels of the construct and test scores. The Messickian validity concept is based on nomological networks and correlations which are problematic because many things in psychology correlate and can fit in a net. They state that defining a construct in relation to other constructs is absurd. Obtaining expected correlations in a net corroborate the theory but does not establish validity. Therefore, the issue of the existence of the construct is not even broached in Messick’s framework. The validity concept advanced by Borsboom et al. [7] is founded on a causal theory of measurement. They state that correlations should be replaced with causality in a validity framework: A test is valid if different levels of the construct cause variations in scores. This implies that the focus of validation should be on the processes or the response behavior which cause these variations and not on the relationship between the measured attribute with other attributes in a nomological net. What constitute validity are the psychological processes that cause variations in test scores and determine the measurement outcome. Validity entails some substantive hypotheses that explain the causal processes that happen between the trait and test scores. Without a theory of response processes it is very hard to find out where the test scores come from [7]ⁱ.

Validity is a measurement concept and discussions of validity only make sense when the measurement theory one adheres to is defined. “…the semantics of validity cannot be separated from the notion of measurement” ([9], p. 328). Meaning can be assigned to validity when the measurement system one thinks is correct is specified. Therefore, a brief discussion of the two most popular measurement models in psychology and education, namely, the classical test theory (CTT) and the latent trait theory, is in order.

The classical test theory (CTT) is the oldest test theory that has served psychology for a century. In this theory, it is assumed that the observed score (X) is composed of a true score (T) and a random error component (e).

X = T + e

The true score in CTT is defined as the mean of the observed scores of a person if she takes a test an infinite number of times, assuming that the memory of each administrations can be wiped out. It contains the non-error systematic factors that the test measures but not what was intended to be measured.

The variance (σ²) of the observed score equals the sum of the variances of the true score and the error score.

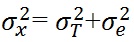The formulation of true score is very convenient to define reliability as the proportion of true score variance to observed score variance.

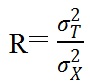This equation is a signal to noise ratio and is the most important contribution of CTT to test analysis. As the variance of the true score increases the reliability augments. The square root of reliability is the correlation between observed scores and true scores.

True score, as might wrongly be thought of, is not the indicator of the real ability we want to measure. The true score reflects the non-error systematic factors that the test actually measures, not what we intended to measure. In many or perhaps most tests, certain unintended and unwanted factors creep into the measurement. Their influence becomes part of the true score variance, adulterating the true score. Psychometrically speaking, true score is the average score of a person if s/he takes a test an infinite number of times assuming that s/he does not get tired and we can wipe off the memory of the previous administrations in every new administration of the test.

Classical test theory assumes that in such a situation the measurement error approaches zero [10]. Therefore, true score is a consistency concept and is not concerned with the measurement of the construct of interest and measurement error is inconsistency of measurement.

Therefore, under the CTT an underlying ability is not assumed and the observed score is just a ‘numerical trick’ to simplify the observations; it carries nothing beyond the content included in the test. In the CTT the so called construct score is only the simplification of observations summarized in a sum score. This position is logically absurd as it is hard to defend statements such as “there is a sum score underlying the item responses” ([11], p. 207). This view is an operationalist position which argues that the operations which are employed to measure concepts are the essence of those concepts. Accordingly, there can never be two different tests of the same construct as each test contains distinct operations (items). Even different combinations of items within the same test measure different constructs. Holding this position, there cannot not be any unidimensionality or test equating. Furthermore, this position is starkly in contrast to the spirit of psychoeducational testing. No one would develop a test to measure a limited content that is included in a test. A test is developed to generalize beyond a specific content and a testing time to a wider domain in the real life non-test situations.

The other measurement model which has gained popularity in the measurement circles in psychology and education is the family of latent trait or latent variable models. A latent variable model is a model which relates observed variables to a latent structure via a mathematical function. Latent variable analysis rests on the co-variation between the observed variables that is taken to indicate a ‘common cause’ or a real entity which can independently be identified as a variable with, in some cases, a biological basis [12]. To put it simply, co-variation among a set of test items indicate something out there, a construct, an attribute, or a skill that has caused the co-variation.

For example, in research on the nature of second language proficiency the general proficiency factor or g is considered to be the common cause of the correlations among tests of language skills and components (grammar, vocabulary, reading, pronunciation, etc.) [13]. In other words, there is an ability in the real world called general proficiency factor which underlies performance on the test items and has caused the correlation among the test items. In psychometric literature the test items are referred to as observed variables or indicators and the variables which causally determine the performance on the test items as latent traits. This means that latent traits which are some mental constructs, such as language proficiency or intelligence, cause performance on the items. In factor analysis one tries to detect and define this common cause by analyzing individual differences and relating co-variation among observed variables to latent variables.

Note that the distinction between observed and latent variable is very subtle. Observed variable does not imply that the variable is really observable. Age in psychological research is treated as an observed variable. However, one cannot claim that the age of a person is seen or the age of a person is on our desk. Age, just like anxiety, is reduced into a number with which researchers can do arithmetic. What makes a latent variable distinct from an observed variable is the certainty involved in the inferences made. When one says that the height of a person is 1.75 m it is certain that the person involved is 1.75 m tall. But when one says that a person’s English language proficiency, as measured by the TOEFL, is 500 one cannot be certain about her level of proficiency. Therefore, the structure of a variable (whether latent or observed) is not intrinsically built into it. With the advancement of measurement methods, latent variables of today might in the future be observed variables [14].

The fundamental question posed by Borsboom et al. [9, 11] is on the nature of latent variables. Are latent variables real entities or some fictions constructed by the researcher? Do they really underlie the observed variables and cause them or are just made out of them? Borsboom et al. ([9], p. 204) state that “(…) without a realist interpretation of latent variables, the use of latent variables analysis is hard to justify”. In other words, they believe that latent variables are real entities which exist independent of measurement. They further argue that this realist view entails a causal relationship between latent variables and observed variables.

This realist view has been voiced by other researchers too. Edwards and Bagozzi ([15], p. 157) argue that “(…) we intend that constructs refer to phenomena that are real and exist apart from the awareness and interpretation of the researcher and the person under study”. But note that “(…) although constructs refer to real phenomena constructs themselves are not real in an objective sense…they are elements of scientific discourse that serve as verbal surrogates for phenomena of interest”. To support a realist view for latent variables Borsboom et al. [9] invoke causality and define a common cause relationship between the latent trait and its indicators. That is, the latent variable is the common cause of its indicators.

There is also a constructivist view which says that latent variables are the construction of human mind and are made out of the data. That is, latent variables have no independent existence and are simply made out of the observed variables. This idea implies that “(…) the relation between the latent variable and its indicators is purely logical. (…) people construct this relation themselves; it is not an actual but a mental relation, revealing the structure of the theories rather than a structure in reality” ([11], p. 211).

There are a number of latent variable models more commonly used in psychological research including the linear factor models [16], Item Response Theory (IRT) models [17, 18], latent class models [19], and mixture models [20]. In the linear factor model both the latent variables and the observed variables are continuous. In IRT, the latent variables are continuous and observed variables are categorical, while in latent class models both the observed and the latent variables are categorical. In the mixture model the observed variables are continuous and latent variables are categorical [14]. The structure of latent variables in psychology can be probed by comparing the fits of these models to data. This might be problematic though as several latent trait models may fit the data equally well [21].

Defining validity in CTT is problematic as no latent trait is assumed to underlie the measurement [22, 23] and there is no construct score incorporated into the model. Some may argue that the true score which is unobservable in CTT is the equivalent of the latent variable score. True score, in CTT, is the average of the observed scores that a person obtains if she takes a test many times. Thus, true score is a consistency concept and is not concerned with the measurement of the intended construct [24] and, therefore, is not equivalent to the construct score [23]. Since the true score is defined in terms of the observed score the true score is not the construct score. In fact, the construct score is not directly incorporated into the CTT formulation and it is very hard to conceptualize validity under this model.

Unlike CTT, in latent trait models the attribute score is explicitly incorporated into the model. The purpose of latent variable models is to enable us to “make an inference from an observed data pattern to an underlying property”, ([14], p. 29 emphasis in the original). The plausibility of the model can be checked against the observed data with the goodness of fit statistics.

In fact, in latent variable models, two sets of equivalent classes, namely, the data structure or the data patterns (observed scores in a spreadsheet) and the latent variable structure, which is inbuilt in the attribute, are linked [14]. Consider an anxiety measure, with a continuous latent structure, which is composed of several items or observed variables. Responses to the test items comprise the data structure. The latent variable is an unobservable trait or property that can only be inferred through its manifestations. The latent trait is conceived to be in the co-variation among the observed variables. The specific variances left in the observed variables after the shared covariation among them is captured in the latent variable are referred to as error variances.

The underlying property or the latent variable of interest about which researchers want to draw inferences is anxiety. This inference is finding the exact location of individuals on a continuous scale, or the class of specific patients to which they may belong if the structure of the latent variable was hypothesized to be categorical. In other words differences in anxiety levels cause variations on item responses.

The assumption is that there is a nondeterministic causal relation between the observed and latent variables. That is, there is a common cause underlying the co-variation among the observed variables which eliminates their relationship when it is conditioned out. This assumption is referred to as the local independence assumption in the latent variable literature [24]. Factoring out the latent variable the observed variables should be statistically independent. If this condition is satisfied it provides evidence for the thesis that the scores on the indicator variables are caused by a common latent variable. However, note that it does not need to be the latent variable that the researcher intends to measure. Validity exists when the expression “the common cause of variation in these item responses” and “the construct the researcher wants to measure” refer to the same entity in the world. Therefore, the fit of a latent trait model, which means that the local independence holds, indirectly provides the validity evidence for an instrument.

Note that the model test does not only involve the hypothesis that a latent variable exists and affects the measures, but also that it is the only common cause of these measures, i.e., explains all of the covariance and some others. Thus, from the misfit of the model, one cannot conclude that the intended variable does not influence the indicators, just like one cannot be certain from model fit that the model is true. However, the fit of latent variable model test confers evidence upon the hypothesis that the intended construct indeed functions as a common cause, and thus for a part of the validity puzzle. That does not require a hard inference from model fit to truth or falsity of the hypothesis. It is like in any other hypothesis test: one never tests a hypothesis in isolation, but conjoined with several other hypotheses required to achieve empirically testable predictions (e.g.., regarding the distribution of the latent variable, the functional form of the Item Characteristic Curves, etc.). But still the degree to which the model fits do confer evidence on the hypothesis in question, conjoined with other hypotheses that might be described as auxiliary (Borsboom, personal communication, May 2016).

The fundamental question in validity is what kind of relation there should be between the observed variables and the latent structure so that one can claim that the data structure is an observed variable for the latent attribute of interest. This question is fundamental to validity research since in validity researchers aim to argue that the test measures what it should measure. If one can claim that our data structure meets the conditions of an observed variable for a latent variable there is evidence for the validity of the test. One option to make this link is causality. That is, one specifies that variations in observed variables-performance on the items is caused by the latent variable which is the essence of validity in Borsbooms’s [7] model. “Validity concerns measurement, and measurement has a clear direction. The direction goes from the world to the psychologists’ instruments. It is very difficult not to construct this relation as causal” ([7], p. 1066).

Note that the relationship between the observed variables, i.e., the data structure and the latent variable structure in commonly-used latent variable models is probabilistic. That is, one does not expect the common cause to account for all the variation in the observed data. Therefore, conditioning on the latent trait there is still some unique variance in the data which are considered errors or residuals and are expected to be uncorrelated. Furthermore, latent variable models map the variable structure onto the probability of data patterns not the data patterns themselves [14].

Therefore, a fundamental requirement of latent variable models is the assumption of local independence. This requirement states that the error variances or residuals should be uncorrelated [24]ⁱⁱ. That is, when the co-variation among the observed variables is captured in a latent factor the unique variances left in them are random noise and uncorrelated [25]. The fit of a latent variable model does not mean that the items are simply correlated with the latent variable. Many items might correlate with the latent variable but only a subset fit a latent variable model, i.e., for which the assumption of local independence holds [26].

Fit of a latent variable model to data, i.e., if local independence holds, is evidence supporting the hypothesis that a latent variable exists which causes variations in observed responses [11]. Therefore, if a latent variable model fits, i.e., the assumption of local independence holds, it offers some inductive support for the common cause hypothesis. This is the essence of validity according to [7].

In this paper an attempt was made to delineate the link between validity and latent trait models. A brief explanation of the two most popular measurement models, i.e., CTT and latent trait models was given, the shifts in validity paradigm over the past century were briefly reviewed, and the link between validity and latent variable models was explicated. It was made clear that due to the deficiencies inherent in the formulation of CTT validity cannot be explicitly addressed under the CTT. The latent trait models, which are now commonly used in psychological testing, were introduced as the modern rival for CTT. They have the necessary elements to embrace validity in their center. The advantage of latent trait models over the CTT is that the construct score is explicitly built into the models which makes them ideal to address validity concerns. Furthermore these models, unlike CTT, are testable. That is, the assumptions of these models lend themselves to rigorous evaluation via elegant statistical procedures.

Fitting a latent trait model as evidence of validity necessitates adopting, perhaps inadvertently, certain positions as regards our worldview on psychological constructs, validity, and measurement in psychology. When a researcher employs a latent variable model to provide validity evidence for a test s/he accepts that there is a causal relationship between the construct and test scores and adheres to the realist concept of the construct. Latent trait models relate the co-variation in a number of test items to an underlying ability or trait. In these models (if the model is unidimensional) a monotonic relation between scores on a number of observed variables and a latent variable is specified. The probability of correctly answering items depends on the latent attribute. That is, the more competent an examinee is, the higher the probability that she gets more items right.

It is also hypothesized that all the items measure the unidimensional variable. Therefore, the dimension should exhaust all the covariation among the indicators and renders them independent conditionally. There is one universal characteristic for measurement and that is the assumption that there is a trait out there in the real world that causally determines the outcome of measurement and the values that measures will take. If conditional independence meets it means that the latent variable is the common cause of variations on test scores and, therefore, the test is valid. Thus, the fit of a unidimensional Rasch model or a one-factor solution is taken as validity evidence. If, however, the indicators are still correlated after conditioning on the latent trait, the local independence assumption and by implication unidimensionality is violated and the items are not valid indicators of the construct. The structure of latent variable theory makes it the model of choice to address validity as conceptualized by Borsboom et al. [7].

The drawback of latent variable models is the problem of underdetermination or statistical equivalence [22]. If a latent trait model fits, the structure hypothesized for the latent variable is not necessarily correct since there might be many structures for the latent variable that yield the same data pattern. Wood (1978 [22],) demonstrated that the outcome of tosses of a number of coins produces a response pattern (considering the outcome of each toss as an item response) that conforms to the Rasch model. Therefore, the fit of a latent trait model does not necessarily support the existence of a substantive construct [22]. One way to tackle this problem is through experimentation, i.e., find a manipulation that changes the latent variable, and see whether the observed variables change as the model predicts [27].

Furthermore, the reason why the local independence assumption meets for some items is not clear. One explanation is that the latent variable is the common cause of variations in item scores [26]. Although the common cause explanation is logical it does not rule out other explanations. “For instance, the item scores may covary systematically and thus exhibit local independence for other reasons, such as some fundamental law of co-occurrence” ([26], p. 39). If items that tap into different constructs mutually influence each other the resulting covariance matrix will satisfy the requirement of local independent (Van der Mass, et al., 2006, cited in [26]). Nevertheless, the common cause explanation is attractive and more plausible than the fundamental law of co-occurrence [26].