RESEARCH ARTICLE
Analysis of the Ruff 2 & 7 Test of Attention with the Rasch Poisson Counts Model
Mahsa Nadri, Purya Baghaei*, Zahra Zohoorian
Article Information
Identifiers and Pagination:
Year: 2019Volume: 12
First Page: 7
Last Page: 11
Publisher ID: TOPSYJ-12-7
DOI: 10.2174/1874350101912010007
Article History:
Received Date: 29/09/2018Revision Received Date: 16/12/2018
Acceptance Date: 7/1/2019
Electronic publication date: 31/1/2019
Collection year: 2019

open-access license: This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International Public License (CC-BY 4.0), a copy of which is available at: https://creativecommons.org/licenses/by/4.0/legalcode. This license permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
Background:
Attention is a basic neurocognitive function which is a prerequisite for performance on more complex cognitive tasks. The Ruff 2 & 7 test is a well-known measure of attention with a well-supported theoretical and empirical underpinnings.
Objective:
The Ruff 2 & 7 test, has not been subjected to rigorous item response theory analysis yet. The purpose of this research was to examine the fit of the Ruff 2 & 7 test to the Rasch Poisson Counts Model (RPCM).
Methods:
Responses of 138 nonclinical subjects to the Ruff 2 & 7 test were analyzed with the RPCM measurement model using ‘lme4’ package in R. The fit of the individual items (blocks) and the overall test to the model were examined.
Results:
Findings showed that three out of seven scoring techniques fit the Rasch model. The scoring techniques which fitted the model were total number of characters cancelled, total number of characters correctly cancelled, and total number of characters correctly cancelled minus errors of commission.
Conclusion:
Three of the scoring techniques fit the RPCM which support the internal validity of the test when these scoring procedures were employed. Therefore, the Ruff 2 & 7 test is psychometrically uni-dimensional when these three scores are computed.
1. INTRODUCTION
The Ruff 2 & 7 Selective Attention Test [1], known also as the 2 & 7 test, is a paper and pencil cancellation test devised to measure different components of attentional processes. The test is composed of 20 blocks of letters and numbers in which numbers 2 and 7 are targets. Each block contains three lines of digits or a combination of digits and letters. Each line contains 50 characters where participants have to cross out the 10 target characters embedded within each line and ignore the distractors. Fifteen seconds are allotted for each block.
The target characters, i.e., 2’s and 7’s, are presented in two conditions. Ten blocks contain only numbers and 10 blocks contain a combination of capital Roman letters and Arabic numbers. The two conditions are presented alternatingly. The idea behind these two distractor conditions is to measure automatic detection and controlled search [2]. Identifying targets among distractors of a different category, i.e., digits among letters, is an instance of automatic detection or parallel processing while finding targets among distractors of a similar type, i.e., numbers within numbers, is an instance of controlled search or serial processing [3].
Initial analyses of the test by [1] demonstrated high retest reliabilities for different age groups and for the two distractor conditions (between .84 to .97). Participants significantly performed better on the automatic search condition compared to the controlled search condition, which was consistent with the theory [2]. Findings also showed that age and education significantly impacted scores. Mean scores systematically decreased with increased age but improved with increasing number of years at school, while sex was found to be unrelated to performance.
In a follow-up study, Ruff et al. [3] administrated the test to patients with brain injuries. Shallice [4] stated that serial and parallel processing is controlled by different areas of the brain. Serial processing is controlled by the frontal lobes and parallel processing is mostly controlled by posterior parts of the brain. Based on these theories, Ruff, et al. formulated some hypotheses concerning the performance of patients with various cerebral lesions on the two distractor conditions. The findings of their study were consistent with the neuro-psychology literature, hence, contributing to the validity argument for the test.
Divergent and discriminant validity of the 2 & 7 test has also been established. The test is correlated with the Digit Symbol Test of the Wechsler Adult Intelligence Scale-Revised [5] in normals (r = .35–.40; Baser & Ruff, 1987). In a sample of normal and clinical cases, the test correlated at r=.62 with the Map Search and at r=.69 with the Telephone Search from the Test of Everyday Attention (TEA) [6, 7]. The 2 & 7 test also correlates with other TEA subtests which measure attentional switching, divided attention, and sustained attention (r = .30 to –.57; (8)) Bate, Mathias, and Crawford (6). performed factor analysis on a combination of attention tests. The 2 & 7 test loaded on a visual selective attention factor which also included the Symbol Digit Modalities Test [10], the Stroop test [11], and the Map Search and Telephone Search subtests from the TEA. Small correlations have been reported with word fluency (r = .17–.22), and no correlation with other executive functioning tests such as the Wisconsin Card Sorting Test [12] and visual and auditory memory tests [8].
The validity and reliability of the 2 & 7 test has been established using classical test theory methods. However, the fit of the test to Item Response Theory models [13] has not been examined yet. To contribute to the validity literature of the 2 & 7 test, this study aims to examine the fit of the test to the Rasch model. If items in a test measure a single latent ability, “then the Rasch model is the necessary and sufficient conceptualization. If they do not, then the set of items contains a mixture of variables and there is no simple, efficient, or unique way to know their utility for measuring anything” [14]. The fit of the RM indicates that the latent ability is quantitative, and items and the latent ability can be measured on an interval scale with a common unit of measurement [15].
2. METHOD
2.1. Participants and Instrument
The Ruff 2 & 7 test of attention was administered according to the standard procedures to 138 nonclinical Iranian university students (68% female). The age range was between 19 to 52 years (M=24.26, SD=5.64). As mentioned earlier, the test consists of 20 blocks of characters where respondents should cross out 2s and 7s in 15 seconds. This time limit is allotted for each block separately. This structure makes the test optimal for RPCM analysis.
3. RESULTS
The Rasch Poisson Counts Model (RPCM) [16] is selected as the measurement model to analyze the Ruff 2 & 7 test. RPCM is a unidmensional member of the family of Rasch models which is used for speeded tests where counts of correct replies or errors, within each task, are modeled instead of replies to individual items [17, 18]. Such testing conditions arise in speeded neuropsychological or psychomotor tests where respondents have to tick off an unlimited number of items within a fixed time period.
The fit of data to a latent trait model, such as the Rasch model, is evidence that the covariation among the test items is caused by an underlying latent factor which could be the intended construct and is, therefore, considered a validity evidence [19, 20].
RPCM can be applied to the raw counts of successes or the raw counts of errors in each item. Here each block is considered an item. We fitted RPCM to seven different scores derived from the test [8]:
- Error of commission (C; non-target characters cancelled)
- Errors of omission (O; target characters respondents failed to cancel)
- Total errors (TE; C+O)
- Total number of characters cancelled (TN)
- Total number of characters correctly cancelled (CTN)
- Total number of characters correctly cancelled minus errors of commission (CTN-C)
- Total number of characters correctly cancelled minus total errors (CTN-TE)
The ‘lme4’ package [9] in R [21] was used to estimate the model. We estimated seven different RPCM’s separately for each scoring technique. Andersen's [22] likelihood ratio test was employed to evaluate the overall fit of the data to the model by partitioning the sample according to their raw score median. The likelihood ratio test is based on the invariance of the item parameters. If the Rasch model holds the item parameters should be invariant within subsamples of the data [23].
As Table 1 shows only the total number of characters canceled, the total number of characters correctly canceled, and total number of characters correctly cancelled minus errors of commission fit the RPCM and the other scoring techniques are not Rasch scalable. In RPCM the assumption is that the mean and variance are equal. The φ coefficient is the ratio of model implied variance to predicted mean [24]. If φ is equal to one, the assumption is met. If it is smaller than one, under dispersion occurs and if it is above one, over dispersion occurs [18]. When over dispersion occurs, reliability is overestimated while in the case of under dispersion, reliability is underestimated. Table 1 clearly depicts that none of the scoring techniques meets this requirement of the RPCM. Nevertheless, CTN-C is the closest to the ideal value among the three fitting models.
Table 2 depicts the item parameters, their standard errors, and their fit statistics for the three scoring techniques which fit the RPCM. A chi-square type item fit statistic based on binning observed and predicted values showed that none of the items misfit the RPCM in the three scoring procedures which fit the RPCM (df=5, α=0.01).
4. DISCUSSION
The Ruff 2 & 7 test of attention is a short and easy-to-administer measure of both selective and sustained attention. It is based on a well-grounded theoretical framework and is relatively well-researched. The test has sound psychometric properties and its validity has been demonstrated against other criterion measures by providing divergent and discriminant evidence. The aim of the present study was to contribute to the validity literature of the test by examining its fit to a unidimensional Rasch model.
The RPCM was chosen as the psychometric model to fit to the 2 & 7 test. Findings showed that three out of seven scoring technique fit the Rasch model. The scoring techniques which fitted the model were total number of characters cancelled, total number of characters correctly cancelled, and total number of characters correctly cancelled minus errors of commission. The other four scoring procedures, i.e., errors of commission, errors of omission, total errors, and the number of characters correctly cancelled minus total errors did not fit the RPCM. Therefore, the Ruff 2 & 7 test is psychometrically unidimensional when these three scores are computed. None of the 20 blocks which are treated as items in the RPCM analysis misfitted.
| Scoring Technique | 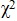 |
df | p | SD | 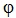 |
Cronbach’s Alpha |
|---|---|---|---|---|---|---|
| C | 46.42 | 19 | 0.00 | 1.26 | .76 | .89 |
| O | 70.87 | 19 | 0.00 | .81 | 1.86 | .95 |
| TE | 71.54 | 19 | 0.00 | .80 | 1.86 | .94 |
| TN | 23.54 | 19 | .21 | .17 | .65 | .93 |
| CTN | 22.43 | 19 | .26 | .17 | .67 | .93 |
| CTN-C | 23.25 | 19 | .22 | .17 | .72 | .94 |
| CTN-TE | 35.86 | 19 | .01 | .17 | 1.93 | .92 |
| Item | TN | CTN | CTN-C | ||||||
|---|---|---|---|---|---|---|---|---|---|
| – | Estimate | SE | Fit | Estimate | SE | Fit | Estimate | SE | Fit |
| 1 | 2.88 | .02 | 14.03 | 2.87 | .02 | 11.13 | 2.87 | .02 | 8.84 |
| 2 | 2.67 | .02 | 1.53 | 2.66 | .02 | 3.51 | 2.66 | .02 | 1.33 |
| 3 | 2.78 | .02 | 5.21 | 2.75 | .02 | 8.03 | 2.75 | .02 | 4.37 |
| 4 | 2.62 | .02 | 14.88 | 2.60 | .02 | 13.24 | 2.60 | .02 | 6.99 |
| 5 | 2.50 | .02 | 6.46 | 2.48 | .02 | 4.78 | 2.48 | .02 | 2.13 |
| 6 | 2.76 | .02 | 2.03 | 2.73 | .02 | 2.76 | 2.73 | .02 | 4.75 |
| 7 | 2.78 | .02 | 1.14 | 2.75 | .02 | 1.30 | 2.75 | .02 | 0.70 |
| 8 | 2.80 | .02 | 2.89 | 2.78 | .02 | 2.65 | 2.78 | .02 | 2.50 |
| 9 | 2.81 | .02 | 5.11 | 2.78 | .02 | 4.96 | 2.78 | .02 | 3.19 |
| 10 | 2.76 | .02 | 6.13 | 2.74 | .02 | 4.87 | 2.74 | .02 | 8.47 |
| 11 | 2.76 | .02 | 8.00 | 2.73 | .02 | 4.56 | 2.73 | .02 | 2.39 |
| 12 | 2.67 | .02 | 8.30 | 2.64 | .02 | 7.97 | 2.64 | .02 | 6.33 |
| 13 | 2.75 | .02 | 2.36 | 2.71 | .02 | 3.39 | 2.71 | .02 | 2.84 |
| 14 | 2.80 | .02 | 1.37 | 2.77 | .02 | 1.00 | 2.77 | .02 | 2.11 |
| 15 | 2.79 | .02 | 2.66 | 2.75 | .02 | 2.63 | 2.75 | .02 | 2.65 |
| 16 | 2.76 | .02 | 3.52 | 2.72 | .02 | 4.14 | 2.72 | .02 | 6.27 |
| 17 | 2.79 | .02 | 0.73 | 2.75 | .02 | 0.76 | 2.75 | .02 | 1.29 |
| 18 | 2.76 | .02 | 2.06 | 2.72 | .02 | 3.42 | 2.72 | .02 | 4.43 |
| 19 | 2.55 | .02 | 5.77 | 2.50 | .02 | 8.66 | 2.50 | .02 | 8.25 |
| 20 | 2.80 | .02 | 1.92 | 2.76 | .02 | 3.36 | 2.76 | .02 | 6.21 |
These findings are in line with another study on the Rasch scalability of the d2 test of attention where researchers demonstrated that the same scoring techniques which showed good fit to the RPCM in this study had also the best fit in the d2 test [25]. In another recent study, Steinborn, et al. [26] examined the reliability of the d2 test and concluded that only the total number of characters correctly cancelled and the total number of characters correctly cancelled minus errors of commission are highly reliable. These scoring techniques were among the best fitting techniques in this study for the Ruff 2 & 7 test.
To date, the 2 & 7 test has mostly been used in English speaking countries or in countries where Latin script and Western style Hindu-Arabic numerals are used. This study examined the performance of a group of respondents who use a different writing system in their native language and is, therefore, not well-accustomed to seeing and scanning Latin letters and Western numerals. The findings suggest that the test is well functioning in the population of such examinees too.
The research has some limitations as well. Since we had a small sample size, we did not investigate measurement invariance and differential item functioning across sex and age groups. Latent trait models in general and IRT models in particular can be used as powerful psychometric models to evaluate neuropsychological tests. The results of the RPCM analysis demonstrated that the 2 & 7 test is an internally valid and accurate measure of attention in a non-western culture. If substantive theory implies that a construct can be represented as a line (i.e. relations between positions on the trait are linearly ordered), and if the items all systematically depend on this construct, without sharing additional variance due to say, direct causal relations or other sources, then one expects that a unidimensional IRT model should fit the data. The fit of a unidimensional IRT model is a backing for the homogeneity of the latent variable. If the latent trait is not homogeneous adding raw scores to compute a total score is not justified because one then adds elements of a heterogeneous trait. Fit of data to the IRT shows that the total raw score is a valid estimator of ability and can be used as an indication of examinees’ latent ability [27].
Future research should examine the utility of the test in clinical samples in non-Latin script cultures.
CONCLUSION
In the classical definition of speed tests, the items are very easy and almost equally difficult. Items in speeded tests have p values above .95 under unspeeded conditions and would be correctly answered by almost everybody [28]. Under such conditions, the application of conventional item response theory models is difficult. RPCM is a model designed for such tests where the total number of items correctly answered or total errors within some time limits on separate parts of the test are modeled instead of individual items. These models are less complex than other IRT models and can be applied with small sample sizes. Analysis, validation, and psychometric evaluation of speeded neuropsychological and psycho-educational tests can benefit from the RPCM.
ETHICS APPROVAL AND CONSENT TO PARTICIPATE
Participation in the study was voluntary. The Institutional Review Board approved the study (IRB decision # 145).
HUMAN AND ANIMAL RIGHTS
All procedures involving human participants were in accordance with the ethical standards of the institutional and/or national research committee and with the 1964 Helsinki declaration and its later amendments or comparable ethical standards.
CONSENT FOR PUBLICATION
All authors made substantial contributions to the work and approved it for publication.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
Declared none.
REFERENCES
| [1] | Ruff RM, Evans RW, Light RH. Automatic detection vs controlled search: a paper-and-pencil approach. Percept Mot Skills 1986; 62(2): 407-16. |
| [2] | Shiffrin RM, Schneider W. Controlled and automatic human information processing: II. Perceptual learning, automatic attending, and a general theory. Psychol Rev 1977; 84: 127-90. |
| [3] | Ruff RM, Niemann H, Allen CC, Farrow CE, Wylie T. The Ruff 2 and 7 Selective Attention Test: A neuropsychological application. Percept Mot Skills 1992; 75(3 Pt 2): 1311-9. |
| [4] | Shallice T. Specific impairments of planning. Philos Trans R Soc Lond B Biol Sci 1982; 298(1089): 199-209. |
| [5] | Wechsler DA. Wechsler Adult Intelligence Scale- Revised: (Manual) The Psychological Corporation 1981. |
| [6] | Bate AJ, Mathias JL, Crawford JR. Performance on the test of everyday attention and standard tests of attention following severe traumatic brain injury. Clin Neuropsychol 2001; 15(3): 405-22. |
| [7] | Robertson IH, Ward T, Ridgeway V, Nimmo-Smith I. The Test of Everyday Attention 1994. |
| [8] | Ruff RM, Allen C. C Ruff 2 and 7 Selective Attention Test professional manual 1996. |
| [9] | Bates D, Maechler M, Bolker B, Walker S, Christensen R, Singmann H, et al. lme4: Linear Mixed-Effects Models using 'Eigen' and S4: R package, version 1 2017; 1-14. |
| [10] | Smith A. Symbol digit modalities test 1973. |
| [11] | Stroop J. Studies of interference in serial verbal reactions. J Exp Psychol 1935; 18: 643-62. |
| [12] | Berg EA. A simple objective technique for measuring flexibility in thinking. J Gen Psychol 1948; 39: 15-22. |
| [13] | Birnbaum A. Some latent trait models and their use in inferring an examinee’s ability.Statistical theories of mental test scores Reading 1968; 395-479. |
| [14] | Wright BD. Misunderstanding the Rasch model. J Educ Meas 1977; 14: 219-25. |
| [15] | Wright BD. Rasch model derived from Campbell concatenation: Additivity, interval scaling. Rasch Meas Trans 1988; 2. |
| [16] | Rasch G. Probabilistic models for some intelligence and achievement tests.Copenhagen: Danish Institute for Educational Research, 1960 1980. |
| [17] | Jansen MG. Rasch’s model for reading speed with manifest explanatory variables. Psychometrika 1997; 62(3): 393-409. |
| [18] | Baghaei P, Doebler P. Introduction to the Rasch Poisson Counts Model: An R Tutorial. Psychol Rep 2018; 33294118797577. Advance online publication |
| [19] | Borsboom D. Latent variable theory. Measurement 2008; 6: 25-53. |
| [20] | Baghaei P, Tabatabaee-Yazdi M. The logic of latent variable analysis as validity evidence in psychological measurement. Open Psychol J 2016; 9: 168-75. |
| [21] | R-Development-Core-Team. A language and environment for statistical computing: Vienna, Austria: R Foundation for Statistical Computing; 2017 [Available from: http: //www.R-project.org/ |
| [22] | Andersen EB. A goodness of fit test for the Rasch model. Psychometrika 1973; 38: 123-40. |
| [23] | Baghaei P, Yanagida T, Heene M. Development of a descriptive fit statistic for the Rasch model. N Am J Psychol 2017; 19: 155-68. |
| [24] | McCullagh P, Nelder JA. Generalized linear models 1989. |
| [25] | Baghaei P, Ravand H, Nadri M. Is the d2 Test of Attention Rasch Scalable? Analysis With the Rasch Poisson Counts Model. Percept Mot Skills 2019; 126: 70-86. |
| [26] | Steinborn MB, Langner R, Flehmig HC, Huestegge L. Methodology of performance scoring in the d2 sustained-attention test: Cumulative-reliability functions and practical guidelines. Psychol Assess 2018; 30(3): 339-57. |
| [27] | Wright BD. Dichotomous Rasch model derived from counting right answers: Raw scores as sufficient statistics. Rasch Meas Trans 1989; 3: 62. |
| [28] | Klein P. The handbook of psychological testing 2000. |







